반응형

문제 풀이
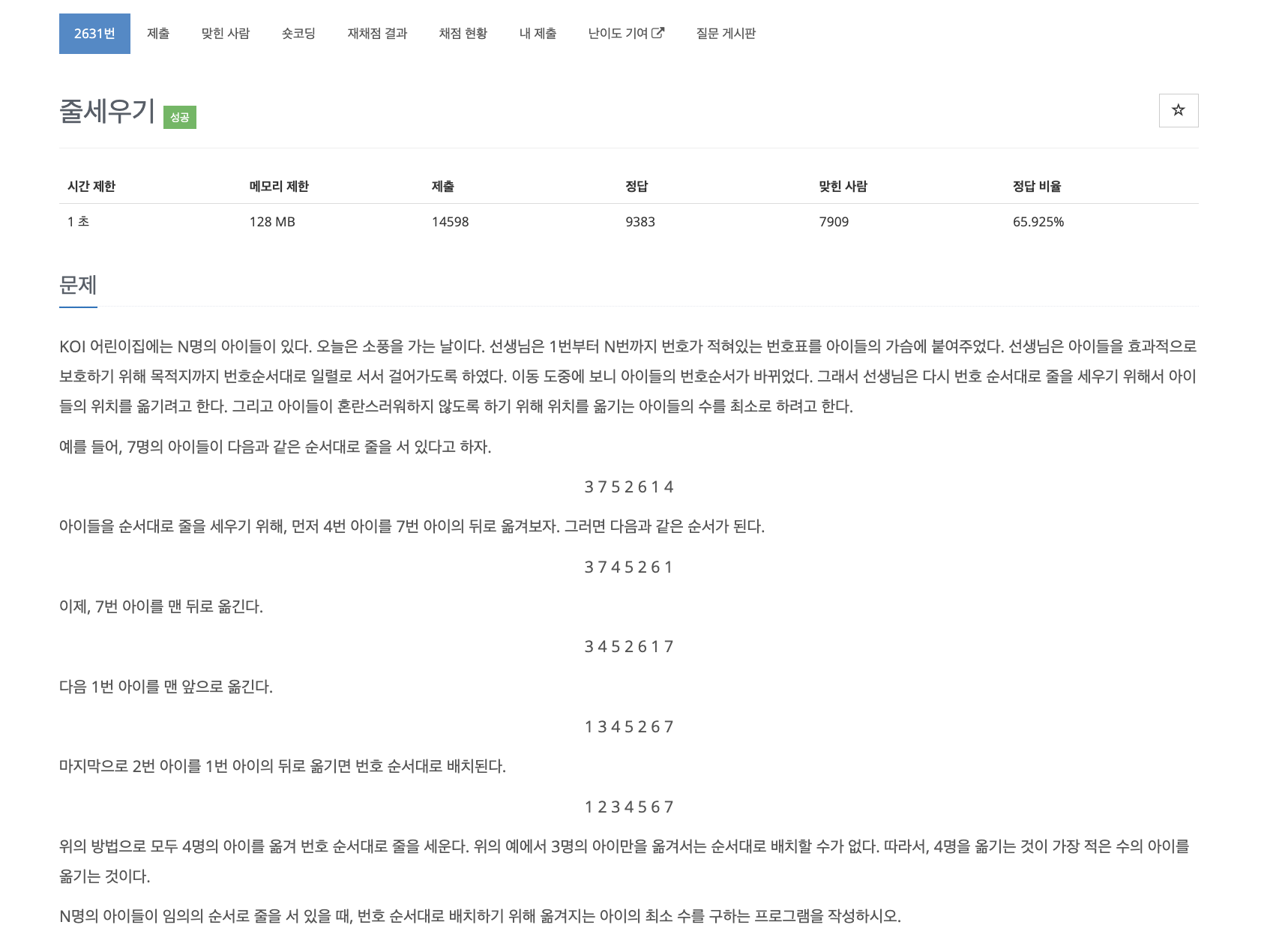
문제 탐색하기
이 문제는 LIS(Longest Increasing Subsequence, 최장 증가 부분 수열) 문제이고 DP알고리즘을 활용하여 풀 수 있습니다.
N명의 아이들이 임의의 순서대로 줄 서 있을 때 최장 증가 수열을 제외한 나머지 아이들을 이동시켜 주면 최소로 이동하면서 번호 순으로 아이들을 줄 세울 수 있습니다.
따라서 최장 증가 수열은 DP 배열의 최대값을 구하게 되면 최장 증가 수열의 수를 카운트 할 수 있고 그 값을 N에서 빼주게 되면 이 값이 바로 아이들을 최소로 이동시키는 수가 될 것 입니다.
DP 배열의 값을 구하는 과정은 현재의 수열의 값을 기준으로 그 전 수열의 값들을 탐색하면서 자신보다 작은 값이 있을 경우 그 때의 DP 배열의 값 + 1 과 자신의 DP 배열의 값을 비교하여 최대값을 다시 저장해주는 순서로 진행됩니다.
이렇게 구한 DP배열에서 최대값을 찾아 N에서 빼주면 그 값이 바로 정답입니다.
문제 풀이
import java.io.BufferedReader;
import java.io.IOException;
import java.util.Scanner;
public class Main {
public static void main(String[] args) throws IOException {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int[] arr = new int[N];
int[] dp = new int[N];
for(int i=0; i<N; i++){
arr[i] = sc.nextInt();
}
dp[0] = 1;
for(int i=1; i<N; i++){
dp[i] = 1;
for(int j=0; j<i; j++){
if(arr[i] > arr[j]){
dp[i] = Math.max(dp[i], dp[j]+1);
}
}
}
int max = 0;
for(int a : dp){
max = Math.max(max, a);
}
System.out.println(N - max);
}
}반응형
'TIL(Today I Learned)' 카테고리의 다른 글
| [TIL] 99클럽 코테 스터디 33일차 TIL + 프로그래머스 신규 아이디 추천 (0) | 2024.11.29 |
|---|---|
| [TIL] 99클럽 코테 스터디 32일차 TIL + 백준 11054 가장 긴 바이토닉 부분 수열 (1) | 2024.11.28 |
| [TIL] 99클럽 코테 스터디 30일차 TIL + 백준 1965 상자 넣기 (0) | 2024.11.26 |
| [TIL] 99클럽 코테 스터디 29일차 TIL + 백준 9461 파도반 수열 (0) | 2024.11.25 |
| [TIL] 99클럽 코테 스터디 28일차 TIL + 백준 11055 가장 큰 증가하는 부분 수열 (0) | 2024.11.24 |



