반응형

문제 풀이
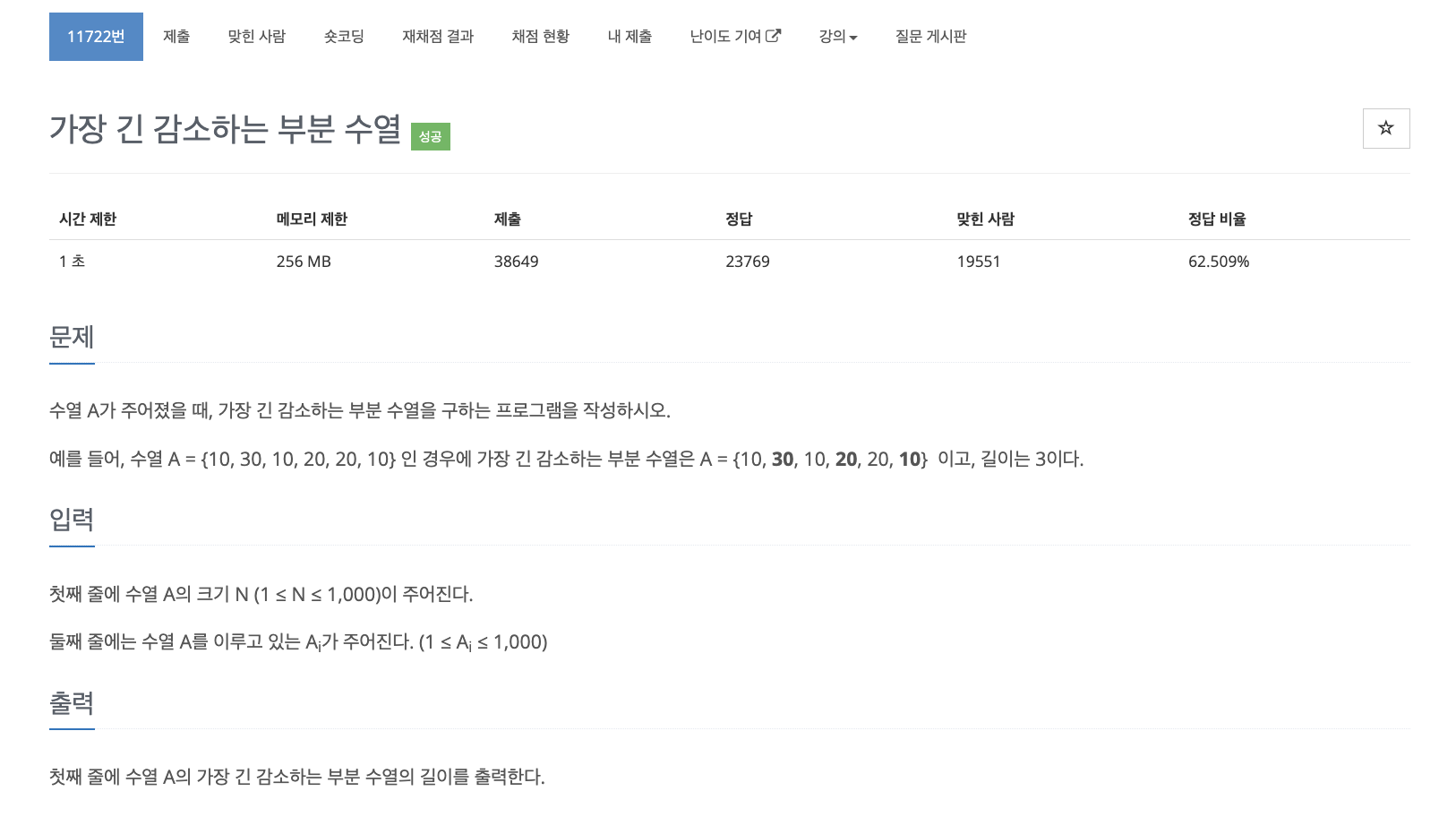
문제 탐색하기
이 문제는 DP 알고리즘을 활용해서 풀 수 있습니다.
DP 알고리즘이란 간단하게는 큰 문제를 작은 단위의 문제로 생각해서 푸는 알고리즘 입니다.
DP 알고리즘
: 이미 계산된 결과는 별도의 메모리 영역에 저장하여 다시 계산하지 않음으로서 수행 시간 단축시키는 방법이며,
DP 구현 방법은 일반적으로 Top-down(하향식)과 Bottom-up(상향식)으로 구성됩니다.
| 탑다운 (Top-Down) | 보텀업 (Bottom-Up) |
| 작은 크기로 문제를 나눠서 해결 | 작은 것부터 해결해서 점차 빌드업 |
| 메모제이션 (memoization) | 타뷸레이션 (tabulation) |
| 일부만 계산해도 답이 나올 때 | 모두 계산해야 답이 나올 때 |
| 재귀 | 반복문 |
| 시간 복잡도 O(n) | 시간 복잡도 O(n) |
DP 알고리즘을 통해 문제 풀이를 구현해 보자면 아래와 같습니다.
- int 배열을 선언해서 수열을 채워줍니다.
- DP 배열을 선언하여 시작을 1로 세팅합니다.
- 현재 값의 이전 값들을 비교해서 현재 값보다 큰 값이 나온다면 그 때의 dp 배열의 값과 현재의 dp 배열의 값을 비교하여 더 큰 값으로 현재 dp 배열의 값을 재세팅 해줍니다.
- 탐색이 종료되면 dp 배열 중 최대 값을 출력해줍니다.
문제 풀이
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int[] arr = new int[N];
int[] dp = new int[N];
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=0; i<N; i++){
arr[i] = Integer.parseInt(st.nextToken());
}
dp[0] = 1;
for(int i=1; i<N; i++){
dp[i] = 1;
for(int j=0; j<i; j++){
if(arr[i] < arr[j]){
dp[i] = Math.max(dp[i], dp[j]+1);
}
}
}
int max = 0;
for(int i=0; i<N; i++){
max = Math.max(dp[i], max);
}
System.out.println(max);
}
}
오늘의 회고
동적계획법에 대해서 접할 수 있는 좋은 기회였던 것 같습니다. 물론 처음 접해보는 유형이라 도움을 받으며 문제를 풀었지만 같은 유형의 문제들을 접하면 혼자서 풀 수 있겠죠....? 퐈이팅
반응형
'TIL(Today I Learned)' 카테고리의 다른 글
| [TIL] 99클럽 코테 스터디 29일차 TIL + 백준 9461 파도반 수열 (0) | 2024.11.25 |
|---|---|
| [TIL] 99클럽 코테 스터디 28일차 TIL + 백준 11055 가장 큰 증가하는 부분 수열 (0) | 2024.11.24 |
| [TIL] 99클럽 코테 스터디 26일차 TIL + 백준 9655 돌 게임 (0) | 2024.11.22 |
| [TIL] 99클럽 코테 스터디 25일차 TIL + 백준 2116 주사위 쌓기 (1) | 2024.11.21 |
| [TIL] 99클럽 코테 스터디 23일차 TIL + 프로그래머스 소수찾기 (0) | 2024.11.20 |



