문제

문제 탐색하기
1. 최소 연산 개수 구하는 규칙 찾기
X를 1부터 7까지 나열하여 최소 연산 개수를 구하는 규칙을 찾아보도록 하겠습니다.
1) X = 1 일때
정수가 주어졌을 때 그 정수를 1로 만들려하는 과정에 사용되는 연산의 횟수의 최소값을 구하는 것이다 보니 연산횟수가 0 입니다.
배열로 생각해보면 arr[0] = 1 로 지정할 수 있습니다.
2) X = 2 일때
X는 2로 나누어 떨어진다면 2로 나누라는 조건에 따라 2로 나눴을 때 1 이됩니다. 연산 횟수는 1, arr[2] = 1
3) X = 3 일때
X는 3으로 나누어 떨어진다면 3으로 나누라는 조건에 따라 3으로 나눴을 때 1이 됩니다. 연산 횟수는 1 , arr[3] = 1
4) X = 4 일때
4를 1로 만드는 경우의 수는 조건에 따라 2가지 입니다.
(첫번째) 2로 나눕니다. 4를 2로 나누면 2가되고 2를 1로 만드는 연산횟수는 이미 앞에서 구한 값입니다. 따라서 연산횟수는 2

(두번째) 1을 뺍니다. 4에서 1을 빼면 3이되고, 3을 1로 만드는 연산횟수도 역시 앞에서 구한 값 1 입니다. 연산횟수는 2
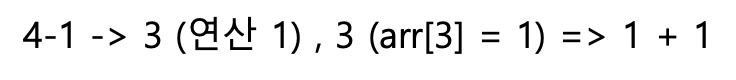
5) X = 5 일때
5는 2와 3으로 나누어 떨어지지 않기때문에 1을 빼는 것을 먼저 진행해줘야합니다.
5에서 1을 빼면 4가 되고 4의 연산횟수는 arr[4] = 2 이므로 총 연산횟수는 3 입니다.
6) X = 6 일때
6은 2또는 3 모두 나누어 떨어집니다. 따라서 3가지 경우의 수를 구해볼 수 있습니다.
(첫번째) 3으로 나눕니다. 6을 3으로 나누면 2가되고 arr[2] = 1 이므로 연산횟수는 2
(두번째) 2로 나눕니다. 6을 2로 나누면 3이되고 arr[3] = 1 이므로 연산횟수는 2
(세번째) 1을 뺍니다. 6에서 1을 빼면 5가되고 arr[5] = 3 이므로 연산횟수는 3입니다.
위 3가지 경우의 수 중 최소값을 구해야하기에 arr[6] = 2 로 저장해주면 됩니다.
7) X = 7 일때
7에서 1을 빼면 6이되고 6을 1로 만드는 연산횟수는 최소 2회이므로 1 + 2 = 3 입니다.
이렇게 X가 1 ~ 7까지 연산횟수를 구해보며 규칙을 찾아보았습니다.
1. X는 3으로 나누어 떨어진다.
2. X는 2로 나누어 떨어진다.
3. X는 3또는 2로 나누어 떨어진다. 즉 6으로 나누어 떨어진다.
4. X는 3또는 2 둘다 나누어 떨어지지 않기에 -1을 해줘야한다.
주어지는 X는 위 4가지 규칙 중 1개에 부합하기에 이 규칙을 바탕으로 연산횟수를 구하면 될 것 같습니다.
2. DP 설계하기
1번에서 최소 연산 개수를 구하는 규칙을 찾으면서 배열에 하나씩 저장하는 과정도 바탕으로 Bottom-Up 방식으로 구현을 해보려합니다.
X를 1로 만들기 위한 최소 연산개수를 구하기 위해 1부터 차례로 구해가면서 이미 구해놓은 작은 문제들의 값을 사용해서 큰 문제를 풀어나가면 될 것 같습니다.
1번에서 찾은 규칙을 바탕으로 아래와 같이 설계해보았습니다.
1) X % 6 == 0 일때 연산횟수
- 1을 빼는 과정 : arr[X-1] + 1
- 3으로 나누는 과정 : arr[X/3] + 1 vs 2으로 나누는 과정 : arr[X/2] + 1 중 최솟값
: (연산 후 값을 배열에 대입해서 찾은 값 + 연산과정 1회) 의 최솟값
2) X % 3 == 0 일때 연산횟수
- 1을 빼는 과정 : arr[X-1] + 1
- 3으로 나누는 과정 : arr[X/3] + 1
: (연산 후 값을 배열에 대입해서 찾은 값 + 연산과정 1회) 의 최솟값
3) X % 2 == 0 일때 연산횟수
- 1을 빼는 과정 : arr[X-1] + 1
- 2으로 나누는 과정 : arr[X/2] + 1
: (연산 후 값을 배열에 대입해서 찾은 값 + 연산과정 1회) 의 최솟값
4) X-1 을 진행해야하는 경우
- 1을 빼는 과정 : arr[X-1] + 1
간단히 코드로 정리해보면 아래와 같습니다.
for(int i=2; i<=X; i++){
if(i % 6 == 0){ // 2 또는 3 으로 나눠 떨어지는 경우
arr[i] = Math.min(arr[i-1], Math.min(arr[i/2], arr[i/3])) + 1;
}else if(i % 3 == 0){ // 3으로 나눠 떨어지는 경우
arr[i] = Math.min(arr[i-1], arr[i/3]) + 1;
}else if(i % 2 == 0){ // 2로 나눠 떨어지는 경우
arr[i] = Math.min(arr[i-1], arr[i/2]) + 1;
}else{ // -1 을 해야하는 경우
arr[i] = arr[i-1] + 1;
}
}
3. 시간복잡도 구하기
arr[X] 의 값을 구하기 위해서 n번 연산을 반복해야하기에 시간복잡도는 O(N) 입니다. N은 최대 10^6 까지 주어질 수 있기에 연산이 1000000개가 진행될 수 있어야 하는데 충분히 시간내에는 가능합니다.
코드 설계하기
- X까지의 최소 연산 횟수를 저장할 배열 선언
- 배열 arr[1] = 0으로 초기값 세팅
- for문을 활용하여 2부터 X까지 DP 구현
- 2 또는 3 으로 나눠 떨어지는 경우, 2또는 3으로 나눈 값의 연산횟수 중 최소 연산횟수를 구하고, 그 연산횟수와 1을 빼서 나온 연산횟수 중 최소 값을 구한 뒤 + 1
- 3으로 나눠 떨어지는 경우, 3으로 나눈 값의 연산횟수와 1을 빼서 나온 값의 연산횟수 중 최소 값을 구한 뒤 + 1
- 2으로 나눠 떨어지는 경우, 3으로 나눈 값의 연산횟수와 1을 빼서 나온 값의 연산횟수 중 최소 값을 구한 뒤 + 1
- 3또는 2로 나누어 떨어지지 않는 경우, 1을 뺀 값의 연산횟수 + 1
- arr[X] 출력
* 2부터 for문을 진행하는 이유 : 1의 초기값 0을 이미 세팅했기 때문입니다.
* 6으로 나누어 떨어지는 경우를 구하는 이유 : 6으로 나누어 떨어지는 경우는 2로 나누어 떨어지는 경우와 3으로 나누어 떨어지는 경우와 1을 빼는 경우 모두 다뤄야하기 때문에 조건식 맨 위에 위치시켰습니다.
정답 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class MakeOne {
public static void main(String[] args) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
int X = Integer.parseInt(reader.readLine());
// 1. X까지의 최소 연산횟수를 저장할 배열 선언
int[] arr = new int[X+1];
// 2. 초기값 세팅
arr[1] = 0;
// 3. DP 구현
for(int i=2; i<=X; i++){
if(i % 6 == 0){
// 3-1. 2 또는 3 으로 나눠 떨어지는 경우, 2또는 3으로 나눈 값의 연산횟수 중 최소 연산횟수를 구하고, 그 연산횟수와 1을 빼서 나온 연산횟수 중 최소 값을 구한 뒤 + 1
arr[i] = Math.min(arr[i-1], Math.min(arr[i/2], arr[i/3])) + 1;
}else if(i % 3 == 0){
// 3-2. 3으로 나눠 떨어지는 경우, 3으로 나눈 값의 연산횟수와 1을 빼서 나온 값의 연산횟수 중 최소 값을 구한 뒤 + 1
arr[i] = Math.min(arr[i-1], arr[i/3]) + 1;
}else if(i % 2 == 0){ // 3-3. 2로 나눠 떨어지는 경우, 2으로 나눈 값의 연산횟수와 1을 빼서 나온 값의 연산횟수 중 최소 값을 구한 뒤 + 1
arr[i] = Math.min(arr[i-1], arr[i/2]) + 1;
}else{ // 3-4. 3또는 2로 나누어 떨어지지 않는 경우 1을 뺀 값의 연산횟수 + 1
arr[i] = arr[i-1] + 1;
}
}
// 4. 출력
System.out.println(arr[X]);
}
}'코딩테스트 챌린지' 카테고리의 다른 글
| [코딩테스트 챌린지] 백준 17204 죽음의 게임 (java) (3) | 2024.09.22 |
|---|---|
| [코딩테스트 챌린지] 백준 10451 순열 사이클 (java) (1) | 2024.09.21 |
| [코딩테스트 챌린지] 백준 1010 다리 놓기 (java) (0) | 2024.09.19 |
| [코딩테스트 챌린지] 백준 2775 부녀회장이 될테야 (java) (0) | 2024.09.18 |
| [코딩테스트 챌린지] 백준 2748 피보나치 수 2 (java) (2) | 2024.09.18 |



